Fediverse
Recently I've been seeing the fediverse logo a lot.
This is the official - yet unofficial - fediverse logo. I liked it, and decided to try to recreate it using procedural code, with Julia. One reason I like to do this is to find out what's easy and what should be easier in the software I write. Another reason is that I often learn something new when working on different designs.
And what is the fediverse?
The fediverse (a portmanteau of "federation" and "universe") is an ensemble of federated (i.e. interconnected) servers that are used for web publishing (i.e. social networking, microblogging, blogging, or websites) and file hosting, but which, while independently hosted, can communicate with each other. On different servers (technically instances), users can create so-called identities. These identities are able to communicate over the boundaries of the instances because the software running on the servers supports one or more communication protocols that follow an open standard. (Wikipedia)
I usually cheat when drawing things like this - straight line caps, white-on-white overlaps, etc. - but this time I thought I'd do it properly, without cheating.
Simple stuff
The first task (doing the easiest first) is to draw the five disks around the edge:
using Luxor, Colors
...
n = 5
R = 210
r = 0.22R
diskcolors = ["#00a3ff", "#9500ff", "#ff0000", "#ffca00", "#64ff00"]
vts = ngon(O, R, n, -deg2rad(9), vertices = true)
for i in eachindex(vts)
sethue(diskcolors[mod1(i, end)])
circle(vts[i], r, :fill)
...I'm using the colors as specified by the original designer. I wondered if they could be algorithmically calculated:
but the differences between a simple calculated set and the original colors suggested to me that the designer tweaked the hues, eg to make a better yellow. A good choice.
The outside connecting edges are built with curves (I'm trying to not cheat), which can be constructed by finding points on surrounding circles.
...
gap = 0.023R
δ = deg2rad(18)
δ1 = deg2rad(22)
disk1 = vts[mod1(i, end)] # the current disk
disk2 = vts[mod1(i + 1, end)] # the next disk
sl = slope(disk1, disk2)
f1 = disk1 + polar(r + gap, sl + δ)
f2 = disk1 + polar(r + gap, sl - δ)
f3 = disk2 + polar(r + gap, π + sl + δ)
f4 = disk2 + polar(r + gap, π + sl - δ)
sidecols = ["#5b36e9", "#d0188f", "#f47601", "#ebe305", "#30b873"]
sethue(sidecols[mod1(i, end)])
newpath()
line(f1)
carc2r(disk1, f1, f2)
line(f3)
carc2r(disk2, f3, f4)
closepath()
fillpath()
...The colors of the outer edges are midway between the colors of the disks they connect. I used Colors.weighted_color_mean() to find the exact middle point between two connected colors, and the differences between my calculated values and the designer's original selections are very small.
I'll use the originals again.
Going deeper
Each of the "interior edges" can be built in two parts, a longer part and a shorter one. I found I had to define quite a few temporary points and construction lines to make these two; I don't know if there's an easier way, but I found myself wishing for some polygon clipping routines...
...
disk3 = vts[mod1(i + 3, end)]
disk4 = vts[mod1(i - 1, end)]
disk5 = vts[mod1(i + 2, end)]
_, crossing = intersectionlines(disk1, disk3, disk4, disk5)
sl1 = slope(disk1, disk3)
sl3 = slope(disk4, disk5)
# the longer edge
g1 = disk1 + polar(r + gap, sl1 + δ)
g2 = disk1 + polar(r + gap, sl1 - δ)
temp1 = disk4 + polar(r + gap, sl3 - δ1)
temp2 = temp1 + polar(5r + gap, sl3)
temp3 = disk4 + polar(r + gap, sl3 + δ1)
temp4 = temp3 + polar(5r + gap, sl3)
temp5 = g1 + polar(distance(g1, crossing), sl1)
temp6 = g2 + polar(distance(g2, crossing), sl1)
_, g3 = intersectionlines(temp1, temp2, g1, temp5)
_, g4 = intersectionlines(temp1, temp2, g2, temp6)
sethue(crosscols[mod1(i, end)])
move(g1)
carc2r(disk1, g1, g2)
line(g4)
line(g3)
line(g1)
fillpath()
# the shorter edge
h1 = disk3 - polar(r + gap, sl1 - δ)
h2 = disk3 - polar(r + gap, sl1 + δ)
_, h3 = intersectionlines(temp3, temp4, g2, h2)
_, h4 = intersectionlines(temp3, temp4, g1, h1)
move(h3)
line(h4)
line(h1)
arc2r(disk3, h1, h2)
line(h3)
fillpath()
...Colors are as specified in the original. And that's it.
Finally
One benefit of having the logo generated procedurally is that it's easier to do silly things with it.
Here's a recursive version, where each disk contains a smaller copy of complete logo.
And it's possible to make various animations:
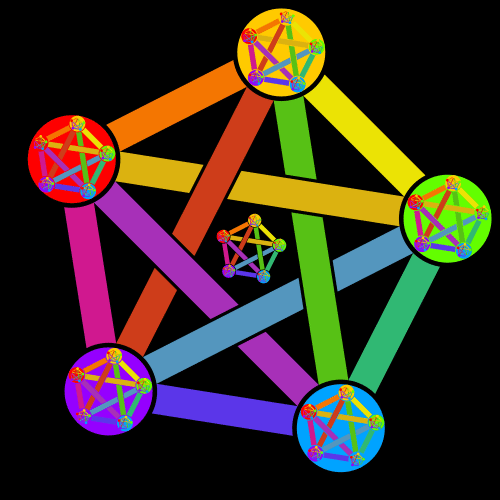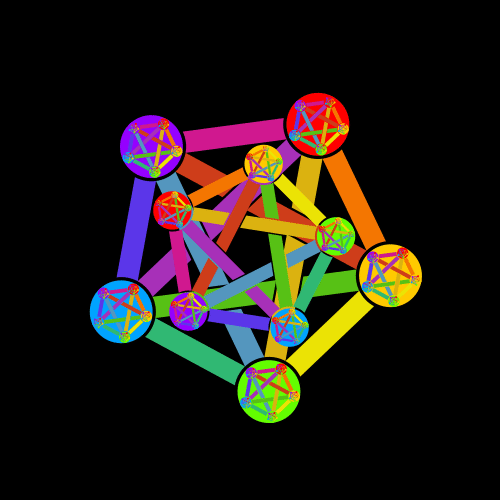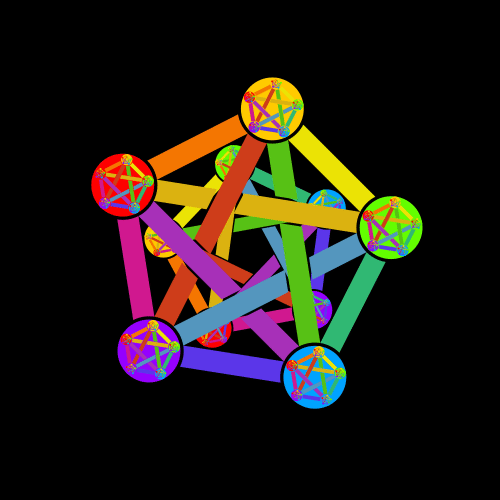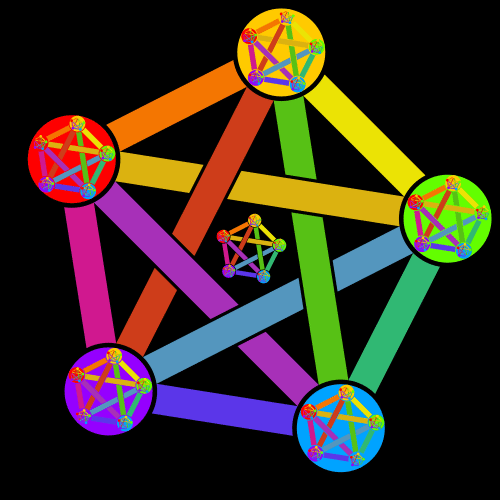
The full code for the logo is here.
using Luxor, Colors
const diskcolors = [
"#00a3ff",
"#9500ff",
"#ff0000",
"#ffca00",
"#64ff00",
]
const sidecols = [
"#5b36e9",
"#d0188f",
"#f47601",
"#ebe305",
"#30b873",
]
const crosscols = [
"#57c115",
"#5496be",
"#a730b8",
"#ce3d1a",
"#dbb210",
]
function fediverse(R, pos = O)
@layer begin
translate(pos)
n = 5
r = 0.22R
gap = 0.023R
δ = deg2rad(18)
δ1 = deg2rad(22)
vts = ngon(O, R, n, -deg2rad(9), vertices = true)
for i in 1:length(vts)
# disks
sethue(diskcolors[mod1(i, end)])
circle(vts[i], r, :fill)
# edges
disk1 = vts[mod1(i, end)] # this disk
disk2 = vts[mod1(i + 1, end)] # the next disk
# outer edges
sl = slope(disk1, disk2)
f1 = disk1 + polar(r + gap, sl + δ)
f2 = disk1 + polar(r + gap, sl - δ)
f3 = disk2 + polar(r + gap, π + sl + δ)
f4 = disk2 + polar(r + gap, π + sl - δ)
sethue(sidecols[mod1(i, end)])
newpath()
line(f1)
carc2r(disk1, f1, f2)
line(f3)
carc2r(disk2, f3, f4)
closepath()
fillpath()
disk3 = vts[mod1(i + 3, end)]
disk4 = vts[mod1(i - 1, end)]
disk5 = vts[mod1(i + 2, end)]
_, crossing = intersectionlines(disk1, disk3, disk4, disk5)
# the longer of the interior edges
sl1 = slope(disk1, disk3)
sl3 = slope(disk4, disk5)
g1 = disk1 + polar(r + gap, sl1 + δ)
g2 = disk1 + polar(r + gap, sl1 - δ)
temp1 = disk4 + polar(r + gap, sl3 - δ1)
temp2 = temp1 + polar(5r + gap, sl3)
temp3 = disk4 + polar(r + gap, sl3 + δ1)
temp4 = temp3 + polar(5r + gap, sl3)
temp5 = g1 + polar(distance(g1, crossing), sl1)
temp6 = g2 + polar(distance(g2, crossing), sl1)
_, g3 = intersectionlines(temp1, temp2, g1, temp5)
_, g4 = intersectionlines(temp1, temp2, g2, temp6)
sethue(crosscols[mod1(i, end)])
move(g1)
carc2r(disk1, g1, g2)
line(g4)
line(g3)
line(g1)
fillpath()
# the shorter of the interior edges
h1 = disk3 - polar(r + gap, sl1 - δ)
h2 = disk3 - polar(r + gap, sl1 + δ)
_, h3 = intersectionlines(temp3, temp4, g2, h2)
_, h4 = intersectionlines(temp3, temp4, g1, h1)
move(h3)
line(h4)
line(h1)
arc2r(disk3, h1, h2)
line(h3)
fillpath()
end
end
end
function draw()
Drawing(600, 600, "/tmp/fediverse.svg")
origin()
background("black")
fediverse(212)
finish()
preview()
end
draw()
[2022-11-14]








